heated atmosphere test for radiative transfer
(pdf version here)
Here we describe the procedure for a test of the Athena++ radiation module where a 1D atmosphere subject to internal heating is allowed to radiatively cool. Eventually, radiative cooling balances internal heating such that a steady-state is reached. This steady-state solution can be obtained by analytic means and compared to the simulation. This test was originally suggested by Zhu & Jiang (2020).
1 Setup
The problem generator ( here) and input file ( here) for this test can be found at the respective links. This test is designed to only test energetics and not dynamics so requires two additional modifications to the source code to effectively turn off hydrodynamics. The first is to remove ‘hydro’ updates to the equations so line 90 of add_flux_divergence.cpp should be commented out.
// update conserved variables pmb->pcoord->CellVolume(k, j, is, ie, vol); for (int n=0; n<NHYDRO; ++n) { #pragma omp simd for (int i=is; i<=ie; ++i) { // u_out(n,k,j,i) -= wght*dflx(n,i)/vol(i); } }
The second is to remove radiation updates to the non-energy (velocity) equations. To do this comment out lines 533-535 in rad_source.cpp.
for (int k=ks; k<=ke; ++k) { for (int j=js; j<=je; ++j) { for (int i=is; i<=ie; ++i) { // u(IM1,k,j,i) += rad_source(1,k,j,i); // u(IM2,k,j,i) += rad_source(2,k,j,i); // u(IM3,k,j,i) += rad_source(3,k,j,i);
with this the problem generator can be compiled
python configure.py --prob=atmosphere_dimensional -implicit_radiation
1.1 Problem Generator
1.1.1 Parameters
The problem takes several input parameters to setup the problem. Required are all the unit condsiderations T_unit, length_unit, density_unit, and molecular_weight which set the initial isothermal temperature, scale height, midplane density, and molecular weight of the atmosphere. These should be set in cgs units in the input file. Then are two problem parameters: the heating rate heatrate and constant opacity opacity which should be supplied in ergs/s/g and cm\(^2\)/g respectively. These are read into the problem generator and converted to code units as follows:
T0 = pin->GetReal("radiation", "T_unit"); H0 = pin->GetReal("radiation", "length_unit"); rho0 = pin->GetReal("radiation", "density_unit"); mol_weight = pin->GetReal("radiation", "molecular_weight"); Real r_ideal = 8.314462618e7/mol_weight; t0 = H0/std::sqrt(r_ideal*T0); // timeunit heatrate = pin->GetOrAddReal("problem", "heatrate", 0.0); opacity = pin->GetOrAddReal("problem", "opacity", 0.0); // make heatrate and opacity dimensionless heatrate *= t0*t0*t0/H0/H0; opacity *= rho0*H0;
1.1.2 Initial Condition
The initial condition is that of an isothermal vertically stratified disk, i.e. gaussian density and pressure profiles. In the code, this looks like:
for(int k=ks; k<=ke; ++k) { for (int j=js; j<=je; ++j) { for (int i=is; i<=ie; ++i) { Real x1 = pcoord->x1v(i); phydro->u(IDN,k,j,i) = exp(-x1*x1*0.5); phydro->u(IM1,k,j,i) = 0.0; phydro->u(IM2,k,j,i) = 0.0; phydro->u(IM3,k,j,i) = 0.0; if (NON_BAROTROPIC_EOS){ phydro->u(IEN,k,j,i) = phydro->u(IDN,k,j,i)/(gamma_gas-1.0); phydro->u(IEN,k,j,i) += 0.5*SQR(phydro->u(IM1,k,j,i))/phydro->u(IDN,k,j,i); phydro->u(IEN,k,j,i) += 0.5*SQR(phydro->u(IM2,k,j,i))/phydro->u(IDN,k,j,i); phydro->u(IEN,k,j,i) += 0.5*SQR(phydro->u(IM3,k,j,i))/phydro->u(IDN,k,j,i); } } } }
We then set the initial condition for the radiation field which we take to be in equilibrium with the gas initial condition (\(I=T^4=1\) in code units).
// Now initialize opacity and specific intensity if (NR_RADIATION_ENABLED || IM_RADIATION_ENABLED) { int nfreq = pnrrad->nfreq; for (int k=ks; k<=ke; ++k) { for (int j=js; j<=je; ++j) { for (int i=is; i<=ie; ++i) { for (int ifr=0; ifr < nfreq; ++ifr) { pnrrad->sigma_s(k,j,i,ifr) = 0.0; pnrrad->sigma_a(k,j,i,ifr) = opacity*phydro->u(IDN,k,j,i); pnrrad->sigma_pe(k,j,i,ifr) = opacity*phydro->u(IDN,k,j,i); pnrrad->sigma_p(k,j,i,ifr) = opacity*phydro->u(IDN,k,j,i); } for (int n=0; n<pnrrad->n_fre_ang; ++n) { // T = 1 everywhere in code units so equilibrium // is given by ir = T^4 = 1 pnrrad->ir(k,j,i,n) = 1.0; } } } } }
1.1.3 Source Term
Internal heating is supplied as a source term. This is the most-appropriate way to do things as opposed to a UserWorkInLoop because source terms are applied during every stage of integration whereas UserWorkInLoop is only applied once after all stages have finished.
void Source(MeshBlock *pmb, const Real time, const Real dt, const AthenaArray<Real> &prim, const AthenaArray<Real> &prim_scalar, const AthenaArray<Real> &bcc, AthenaArray<Real> &cons, AthenaArray<Real> &cons_scalar) { for (int k=pmb->ks; k<=pmb->ke; ++k) { for (int j=pmb->js; j<=pmb->je; ++j) { for (int i=pmb->is; i<=pmb->ie; ++i) { Real x = pmb->pcoord->x1v(i); if (NON_BAROTROPIC_EOS) { cons(IEN,k,j,i) += heatrate*prim(IDN,k,j,i)*dt; } } } } return; }
1.1.4 Boundary Condition
Because the hydrodynamics is not evolved, the boundary condition is not particularly important so we just set it to be an outflow condition.
void DiskInnerOutflowX1(MeshBlock *pmb, Coordinates *pco, AthenaArray<Real> &prim, FaceField &b, Real time, Real dt, int is, int ie, int js, int je, int ks, int ke, int ngh) { for (int n=0; n<(NHYDRO); ++n) { for (int k=ks; k<=ke; ++k) { for (int j=js; j<=je; ++j) { for (int i=1; i<=ngh; ++i) { prim(n,k,j,is-i) = prim(n,k,j,is); } } } } return; }
The radiation boundary condition on the other hand is very important since the steady state solution is essentially a boundary-value problem. We set the boundary condition to be that of a vacuum, in the sense that incoming intensities are set to zero and outgoing intensities are analogous to the standard outflow boundaries of hydrodynamics. We use the variable mu (the angle cosines) to distinguish between ingoing and outgoing rays.
void DiskRadInnerX1(MeshBlock *pmb, Coordinates *pco, NRRadiation *prad, const AthenaArray<Real> &w, FaceField &b, AthenaArray<Real> &ir, Real time, Real dt, int is, int ie, int js, int je, int ks, int ke, int ngh) { int nang=prad->nang; int nfreq=prad->nfreq; for (int k=ks; k<=ke; ++k) { for (int j=js; j<=je; ++j) { for (int i=1; i<=ngh; ++i) { for (int ifr=0; ifr<nfreq; ++ifr) { for(int n=0; n<nang; ++n){ int ang = ifr*nang + n; Real& miux=prad->mu(0,k,j,is-i,n); if (miux < 0.0) ir(k,j,is-i,ang) = ir(k,j,is,n); else ir(k,j,is-i,ang) = 0.0; } } } } } return; }
2 The Analytic Solution
While the code evolves an initial boundary problem, if the code is run long enough the atmosphere will reach a steady state at which point the atmosphere state is determined by a boundary value problem. While the radiative boundary value problem does not in general have an analytic solution, if we run the code using nmu=1 (one upward angle, one downward) we are solving the radiative transfer under a two-stream approximation which does indeed have an analytic solution. In this section we derive the analytic solution for the two-stream steady state heated atmosphere. For background on the two-stream approximation, see the last section of Chapter 1 of Rybicki & Lightman. In the two stream approximation we have \begin {equation} \frac {1}{3}\frac {\partial ^2 J}{\partial \tau ^2} = \epsilon \left (J-B\right ) \end {equation} In steady state, we also have the terms due to radiative cooling/heating equal to heating in the disk \begin {equation} \frac {\partial E}{\partial t} = \underbrace {4\pi (\sigma _a+\sigma _s)\left (J - S\right )}_\text {radiative cooling} + \underbrace {C\rho }_\text {viscous heating} = 0 \end {equation} Where \(C\) is a constant determining the heating rate in the disk. Assuming \(\sigma _s = 0\) gives \(\epsilon \rightarrow 1\) and \(S\rightarrow B\) so, \begin {equation} \frac {1}{3}\frac {\partial ^2 J}{\partial \tau ^2} = J-B = -\frac {C\rho }{4\pi \sigma _a} \end {equation} Replacing with the opacity \(\kappa = \sigma /\rho \), \begin {equation} \frac {\partial ^2 J}{\partial \tau ^2} = \frac {3C}{4\pi \kappa } \end {equation} In steady state we know that the total heating put into the disk must be the same as the heat leaving through the boundaries. The total integrated heat input rate in a column of area \(A\): \begin {equation} \dot {E} = A\int _{-\infty }^\infty C \rho dz \end {equation} which must be equal to the flux emitted at both the upper and lower surfaces of the disk. If we define the flux (i.e. \(\dot {E}/A\)) from one edge of the disk as \(\sigma T_\text {eff}^4\), then because of the midplane symmetry \begin {equation} \sigma T_\text {eff}^4 = \int _0^\infty C\rho dz = C\int _0^\infty \frac {d\tau }{\kappa } = \frac {C\tau _{1/2}}{\kappa } \end {equation} if \(C\), \(\kappa \) are constant and we’ve defined the optical depth to midplane \(\tau _{1/2}\). Substituting the heating rate \(C = \sigma T_{\rm eff}^4\kappa /\tau _{1/2}\) for the flux in Equation 4, we get \begin {equation} \frac {\partial ^2 J}{\partial \tau ^2} = -\frac {3\sigma T_{\rm eff}^4}{4\pi \tau _{1/2}} \end {equation} which can be integrated to find \(J(\tau ), B(\tau )\). Integrating the equation we get: \begin {equation} J = -\frac {3\sigma T_{\rm eff}^4}{4\pi \tau _{1/2}}\frac {\tau ^2}{2} + A_1\tau + A_0 \end {equation} Our first condition comes from the fact that the ingoing flux is \(0\) at the outer boundary. In the two stream approximation, \begin {equation} I^- = J - \frac {1}{\sqrt {3}}\frac {\partial J}{\partial \tau } \end {equation} which at \(\tau =0\) becomes, \begin {equation} \frac {\partial J}{\partial \tau } = \sqrt {3}J \end {equation} Plugging in \(J\) gives, \begin {equation} A_1 = \sqrt {3}A_0 \end {equation} Now we have \begin {equation} J = -\frac {3\sigma T_{\rm eff}^4}{4\pi \tau _{1/2}}\frac {\tau ^2}{2} + A_1\tau + \frac {A_1}{\sqrt {3}} \end {equation} But we also know the flux \(H\) is \(0\) at \(\tau =\tau _{1/2}\). In the two stream approximation (\(3H=d J/d \tau \)) this means: \begin {equation} \frac {\partial J}{\partial \tau } = 0 \end {equation} Which means, \begin {equation} A_1 = \frac {3\sigma T_{\rm eff}^4}{4\pi } \end {equation} Finally we get, \begin {equation} J = -\frac {3\sigma T_{\rm eff}^4}{4\pi \tau _{1/2}}\frac {\tau ^2}{2} + \frac {3\sigma T_{\rm eff}^4}{4\pi }\tau + \frac {1}{\sqrt {3}}\frac {3\sigma T_{\rm eff}^4}{4\pi } \end {equation} Or, \begin {equation} J = \frac {3\sigma T_{\rm eff}^4}{4\pi }\left [ \tau \left (1-\frac {\tau }{2\tau _{1/2}}\right ) + \frac {1}{\sqrt {3}}\right ] \end {equation} Also because \(J-B=J-\sigma T^4/\pi =-C/4\pi \kappa = -\sigma T_\text {eff}^4/4\pi \tau _{1/2}\), \begin {equation} T = \left (\frac {\pi J}{\sigma } + \frac {T_\text {eff}^4}{4\tau _{1/2}}\right )^{1/4} \end {equation} \begin {equation} T = \left ( \frac {3 T_{\rm eff}^4}{4}\left [ \tau \left (1-\frac {\tau }{2\tau _{1/2}}\right ) + \frac {1}{\sqrt {3}} + \frac {1}{3\tau _{1/2}}\right ]\right )^{1/4} \end {equation} where again \(T_\text {eff}^4\equiv C\tau _{1/2}/(\sigma \kappa )\)
3 Running the Test
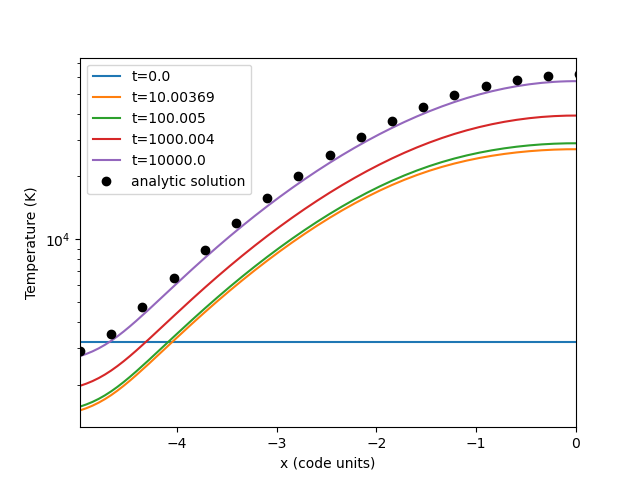
Try running the test problem, it should take about \(\sim 5\) minutes on a single core standard laptop. You can make a plot like Figure 1 of the temperature evolving to steady state and compare with the analytic solution (python plotting script here).
4 Exercises
Here are some extensions to this test that you can try.
- The default problem simulates both the upper and lower halves of the disk, try instead to simulate the upper half of the disk with a reflecting boundary at the midplane. Confirm the solutions are identical between setups.
- The steady state solution does not depend on the initial condition, only on the optical depth distribution and the heating rate. Confirm that different initial conditions will produce the same steady state so long as the product of \(\rho \kappa \) and the heating rate are unchanged.
- While we have an analytic solution to this case with two angles (nmu=1), we do not have one in general. Run the problem with many more angles and see how well this two-stream approximation works compared to reality. See if the magnitude of this discrepancy changes as you change the opacity from optically thick to optically thin.
- The analytic solution does not depend on having a vertical-disk like structure and applies to any fixed density/opacity distribution. Modify the problem generator to instead use an initial condition for a isothermal atmosphere under a constant gravitational acceleration (i.e. exponential) with terrestrial parameters (\(T_0 = 300\) K, \(\rho _0 = 10^{-3}\) g/cm\(^3\), \(g=100\) cm/s\(^2\)).
Don’t forget to uncomment the changes made to the source code when you’re done with this test.